Scaling Up/Out Embarrassingly Parallel Problems in R¶

By: Naeem Khoshnevis
Last Update: June 9, 2022

Problem statement¶

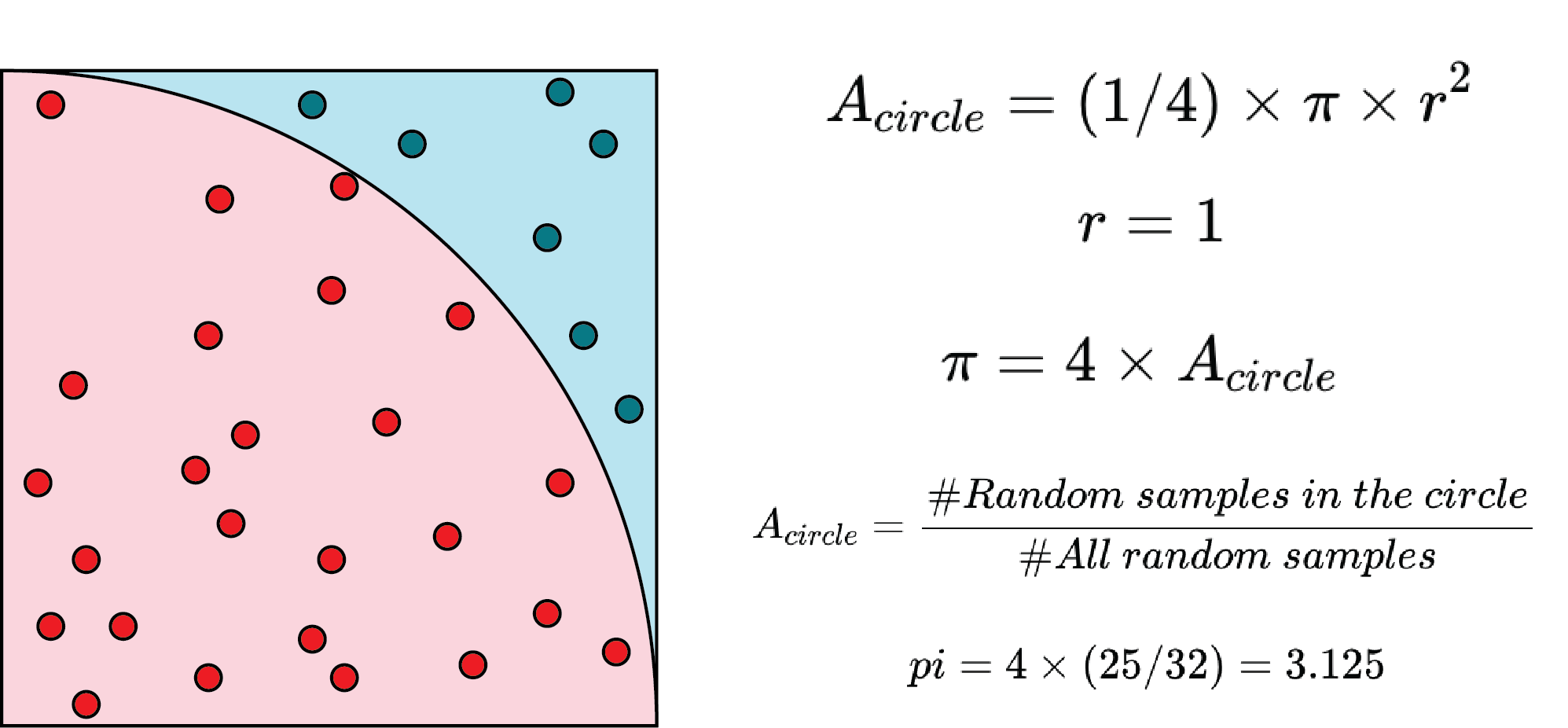
Estimating PI has always been an interesting problem, and many algorithms have been proposed. One of the methods is the Monte Carlo approach, which is a perfect fit for testing embarrassingly parallel problems. According to the following figure and equations, the estimation of PI can be achieved by drawing random samples.

There are two approaches to improve the results:

Increasing the number of random samples, and
Repeating the test.

We are using both approaches.

Solutions based on computational resources¶

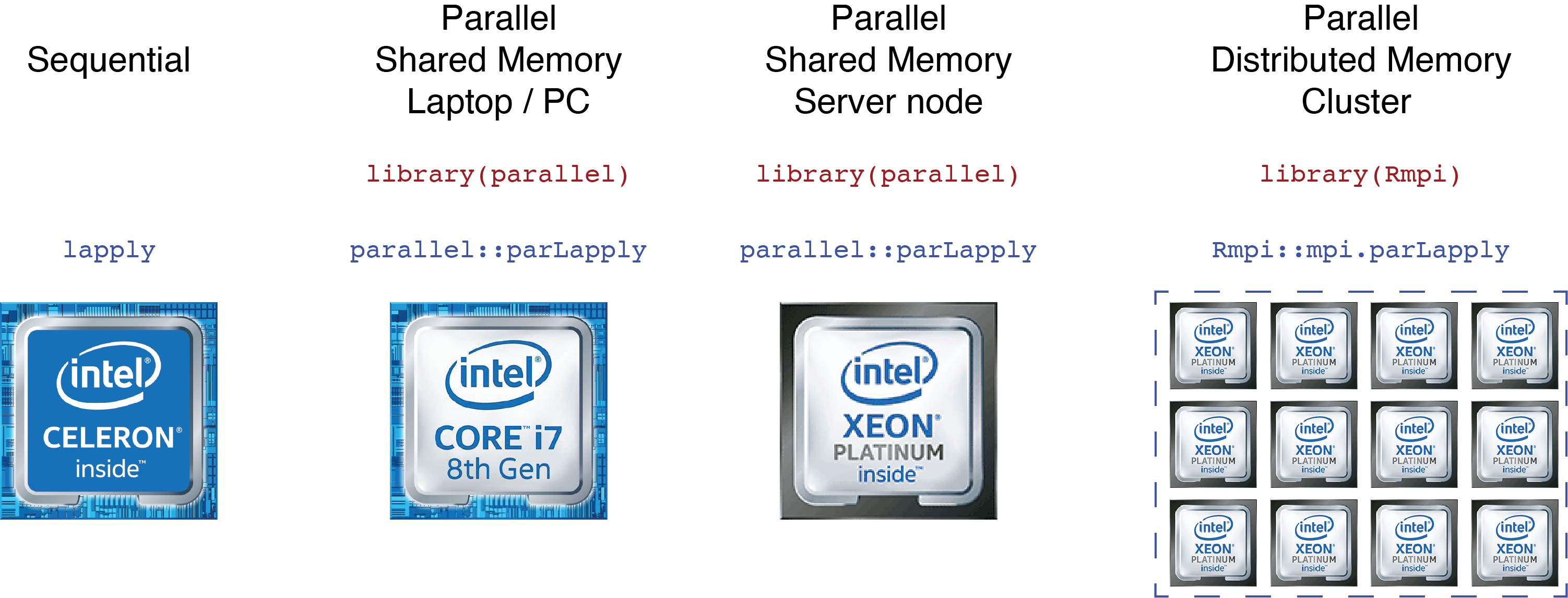
Most of the statistical analyses can be considered embarrassingly parallelizable problems (Monte Carlo estimations, Bootstrap analyses, …). We present four different solutions based on available computational resources. This clarifies the steps on how to tailor the code based on these resources.

Estimating PI¶

Different approaches can be used to solve the problem. However, we use lapply because it makes the comparison easier. Here is the function to compute pi.

mc_pi <- function(sample_size){
  
  set.seed(as.integer(proc.time()[[3]]*1000))
  x <- runif(sample_size)
  y <- runif(sample_size)
  z <- sqrt(x^2+y^2)
  pi <- (length(which(z<=1))*4)/length(z)

  return(pi)
}

To facilitate understanding the accuracy of the results, we count the number of matched digits between actual and estimated PI.

# PI : http://www.geom.uiuc.edu/~huberty/math5337/groupe/digits.html
PI <- 3.14159265358979323846

match_chars <- function(number_1, number_2){
  
  sn1 <- strsplit(sprintf("%.54f", number_1),"")[[1]]
  sn2 <- strsplit(sprintf("%.54f", number_2),"")[[1]]
  
  i <- 1
  l <- min(length(sn1), length(sn2))
  
  for (i in seq(1,l)){
    if (sn1[i] != sn2[i]){
      return(i-1)
    } else {
      i <- i + 1
    }
  }
  return(i-1)
}

Sequential¶

The sequential approach uses one core. The lapply version of the code is according to the following:

n <- 1000  # number of samples in each trial
m <- 1000000 # number of trials.

trial_vec <- (numeric(m)+1)*n

t1 <- proc.time()
pi_list_tmp <- lapply(trial_vec, mc_pi)
t2 <- proc.time()

print(paste("Processing time: ",t2[[3]] - t1[[3]], " s."))

pi_list <- c(do.call(rbind, pi_list_tmp))
pi <- mean(pi_list)

options(digits=20)
print(paste("PI value: ", PI))
print(paste("Est.  pi: ", pi))
print(paste("Number of matched chars: ", match_chars(pi, PI)))

Parallel on a laptop computer (Shared Memory)¶

The parallel version of lapply comes in different formats (mclapply vs parLapply). The main difference is the method of spawning new processes. We recommend using parLapply. Although it has slightly more overheads, it works on all systems, including macOS, Windows, and Linux flavors.

library(parallel)

n <- 1000  # number of samples in each trial
m <- 100000 # number of trials.

trial_vec <- (numeric(m)+1)*n

# create cluster of workers
nthread <- 12
cl <- parallel::makeCluster(nthread, type="PSOCK")

t1 <- proc.time()
pi_list_tmp <- parallel::parLapply(cl, trial_vec, mc_pi)
t2 <- proc.time()

parallel::stopCluster(cl)

print(paste("Processing time: ",t2[[3]] - t1[[3]], " s."))

pi_list <- c(do.call(rbind, pi_list_tmp))
pi_mean <- mean(pi_list)

options(digits=20)
print(paste("PI value: ", PI))
print(paste("Est.  pi: ", pi_mean))
print(paste("Number of matched chars: ", match_chars(pi_mean, PI)))

Parallel on a Server Node (Shared Memory)¶

The parallel version of the solution on a server node is the same as on a laptop. The server node is more or less similar to a laptop or a desktop computer; however, it has a higher number of cores and bigger memories (including a bigger cache). You can see the steps to test the code on FASRC Virtual Desktop Infrastructure in the following link.

Estimating PI on a FASRC server node

Parallel on Multiple Nodes (Distributed Memory)¶

Going beyond one node requires some infrastructure. In other words, the nodes should be able to communicate with each other. The most commonly used paradigm is using Message Passing Interface (MPI). For R processes in this example, we use Rmpi, which is a wrapper for OpenMPI library. For setting up the environment, please visit the following link:

Install and Set Up Rmpi in the User Environment

Rmpi supports parLapply through the parallel package. The advantage of using mpi is going beyond one server node. Here is the modified version of the code (parLapply_mpi.R).

# Load the R MPI package if it is not already loaded.
if (!is.loaded("mpi_initialize")) {
    library("Rmpi")
    }

#
# In case R exits unexpectedly, have it automatically clean up
# resources taken up by Rmpi (slaves, memory, etc...)
.Last <- function(){
       if (is.loaded("mpi_initialize")){
           if (mpi.comm.size(1) > 0){
               print("Please use mpi.close.Rslaves() to close slaves.")
               mpi.close.Rslaves()
           }
           print("Please use mpi.quit() to quit R")
           .Call("mpi_finalize")
       }
}

n <- 1000000  # number of samples in each trial
m <- 100000000 # number of trials.
val <- (numeric(m)+1)*n

time_a <- proc.time()
pi_list_tmp <- mpi.parLapply(val, mc_pi)
time_b <- proc.time()

print(paste("Processing time: ",time_b[[3]] - time_a[[3]], " s."))

pi_list <- c(do.call(rbind, pi_list_tmp))
pi_hat <- (mean(pi_list))

options(digits=20)
print(paste("PI value: ", PI))
print(paste("Est.  pi: ", pi_hat))
print(paste("Number of matched chars: ", match_digit(pi_hat, PI)))

# Tell all slaves to close down, and exit the program
mpi.close.Rslaves(dellog = FALSE)
mpi.quit()

You can submit a job using the following submission file (run.sh).

#!/bin/bash
#SBATCH -J mpi
#SBATCH -o %j_job.out
#SBATCH -e %j_job.err
#SBATCH -p shared
#SBATCH -n 100
#SBATCH -t 50
#SBATCH --mem-per-cpu=4000

# Load required software modules 
module load R/3.5.1-fasrc01
module load gcc/10.2.0-fasrc01 openmpi/4.1.1-fasrc01

# Set up Rmpi package
export R_LIBS_USER=$HOME/apps/R/3.5.1:$R_LIBS_USER
export R_PROFILE=$HOME/apps/R/3.5.1/Rmpi/Rprofile

# Run program
export OMPI_MCA_mpi_warn_on_fork=0
srun -n 100 --mpi=pmix R CMD BATCH --no-save --no-restore parLapply_mpi.R

In your login node, you can submit the job.

sbatch run.sh

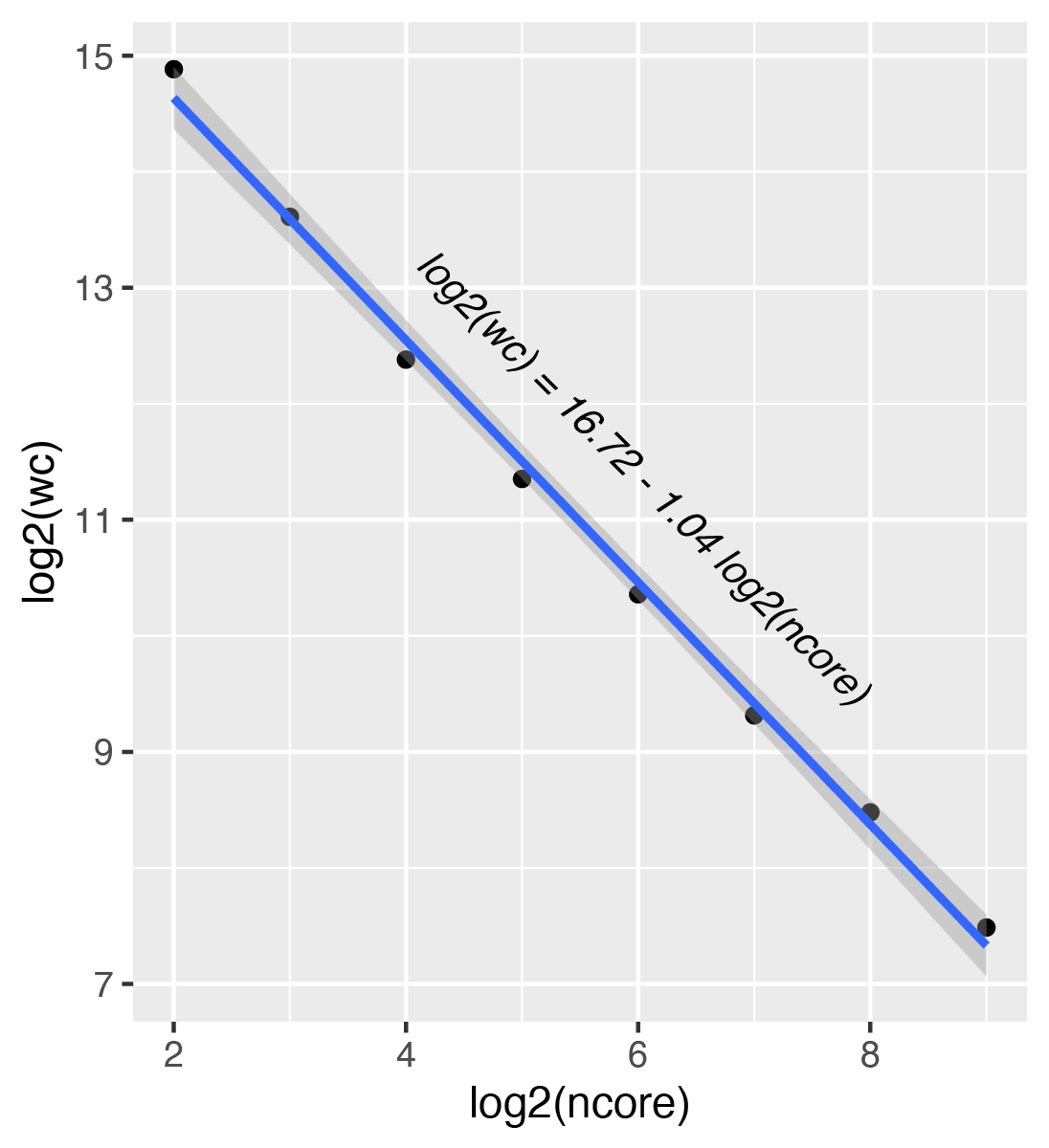
The following figure shows scaling the job among different number of cores and corresponding wall clock time. The results show a perfect linear scaling.

#cores (ncore)	Wall Clock Time in s (wc)
4	30215.443
8	12509.134
16	5331.597
32	2613.654
64	1312.239
128	636.674
256	356.642
512	179.275

NSAPH Software

Scaling Up/Out Embarrassingly Parallel Problems in R

Contents